1. Obrazem kružnice procházející bodem J je přímka.
Kružnice procházející bodem J leží v rovině, která prochází bodem J. Tato rovina protne rovinu ω v přímce a na ní budou ležet obrazy bodů původní kružnice.
2. Obrazem kružnice neprocházející bodem J je kružnice.
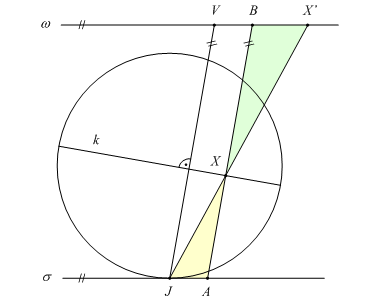
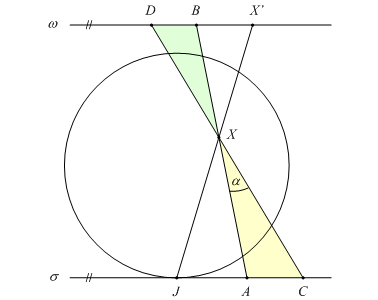
 | obr.1a - případ vedlejší kružnice Konstrukce znázorňuje kužel s vrcholem V dotýkající se sféry na kružnici k. Bod X leží na této kružnici a přímka JX zobrazuje bod X na X'. Přímka VX se dotýká sféry v bodě X a protíná rovinu σ v bodě A. Z něj vedou ke sféře dvě tečny, takže |AJ| = |AX| a díky podobnosti trojúhelníků AXJ a VXX' též |VX'| = |VX|. Tato vzdálenost je však stejná pro všechny body kružnice k. Jejím obrazem je tedy kružnice se středem ve vrcholu V. |
 | obr.1b - případ hlavní kružnice Konstrukce znázorňuje přímku JV kolmou k rovině hlavní kružnice k. Bod X leží na této kružnici a přímka JX zobrazuje bod X na X'. Přímka AB se dotýká sféry v bodě X a je rovnoběžná s JV. Přímky JV, AB a JX' leží v jedné rovině. Protože |VB| = |JA| = |XA| a |BX'| = |BX|, dostáváme pro délku |VX'| = |VB| + |BX'| = |AB| = |JV|, tedy hodnotu stejnou pro všechny body kružnice k. Jejím obrazem je tak kružnice se středem v bodě V. |
3. Stereografická projekce je zobrazení konformní (úhlojevné).
 | obr.2 Bod X je bodem sféry a X' je jeho obraz. Přímky AB a CD se dotýkají sféry v bodě X a svírají úhel α. V rovině ω jsou jejich obrazem přímky BX' a DX'. Ukážeme, že i tyto obrazy svírají úhel α. Tento úhel je díky podobnosti dvou čtyřstěnů roven úhlu při vrcholu J v trojúhelniku AJC, který navíc je shodný s trojúhelníkem AXC (|JA| = |XA| a |JC| = |XC|). Úhel, pod kterým se protínají dvě na sféře ležící křivky, zůstává v projekci stejný. Projekcí limitně malého sférického trojúhelníka je tedy trojúhelník podobný – stereografická projekce je zobrazení konformní. |