
This brief text deals with some issues related to the geometry of the astrolabe of the Prague Astronomical Clock. Rich and interesting history of the Orloj and a detailed description of its parts can be found in a long series of works dedicated to it both printed and on the Internet. Those interested in this field may well use extensive collection of documents, pictures and links available at http://www.orloj.eu.
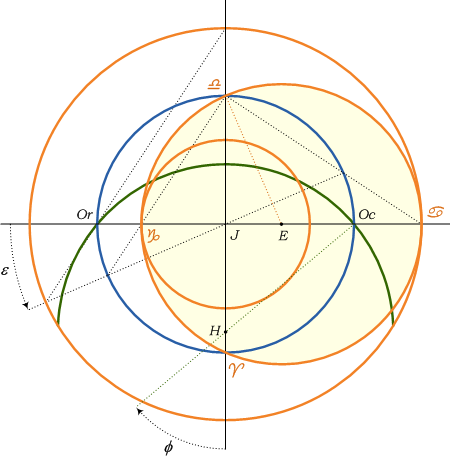
The sky displayed on the Orloj is based on the stereographic projection of the celestial sphere from its North Pole to the equator plane. The advantage of this design is that the sky appearance is comprehensible and the orientation corresponds to looking at the real sky midday-wise. In the centre of the astrolabe is an image of the South Pole. Basic geometric properties of this projection, known for over two thousand years, are derived here, among others. The structure below shows the basic elements of the astrolabe together with a derivation of theirs dimensions:

All dimensions are determined by the obliquity of the ecliptic ε and geographic latitude φ. Unit of length is the radius of the celestial equator (blue circle).
| Radius of the Tropic of Capricorn | = | tg(45° – ε/2) |
| Radius of the Tropic of Cancer | = | tg(45° + ε/2) |
| Radius of the ecliptic | = | 1/cos(ε) |
| Distance from the south pole to the centre of ecliptic | = | tg(ε) |
| Radius of the horizon | = | 1/sin(φ) |
| Distance from the south pole to the centre of horizon | = | cotg(φ) |
Solar raffia of the Prague Astronomical Clock rotates at the constant angular velocity one revolution per mean solar day. Dial of Roman numerals divided into two twelve hour sets (German time) allows one thus to read the mean solar time that is set to match the Central European Time. Digital model shows not the mean, but the real rectascension of the Sun; hour angle of the vernal equinox (sidereal time) is that of Prague. Digital model shows the true solar time at the Prague meridian.
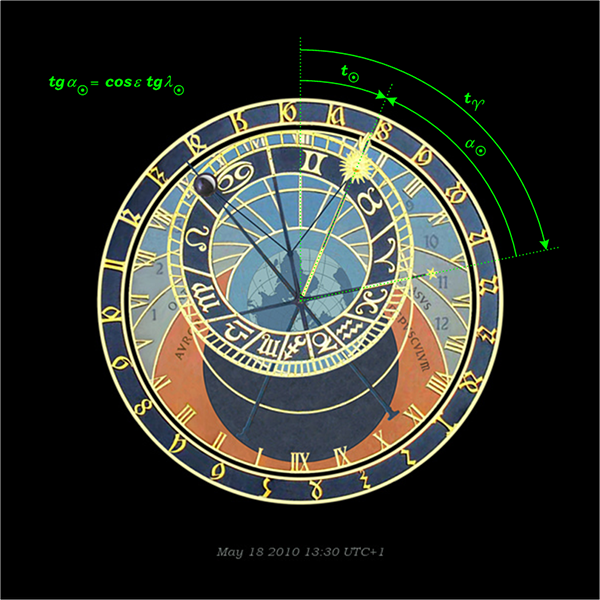
Ecliptic on the astrolabe is represented by the outer ring of the zodiac. The Sun should be placed on the ecliptic but due to historical reasons, the bars that keep the Sun and Moon in the zodiac are shorter. This fault is reproduced on the model to maintain similarity to the Orloj.
The scale of the zodiac allows reading ecliptic longitudes. The following picture shows the stereographic projection of the ecliptic, including its south pole. The great circles of constant ecliptic longitude cross at this pole and divide the zodiac into twelve zodiacal signs of the same ecliptic length. The corresponding rectascensions are no longer multiples of thirty degrees. Respective values of right ascension of points on the ecliptic can be found from the relationship below.
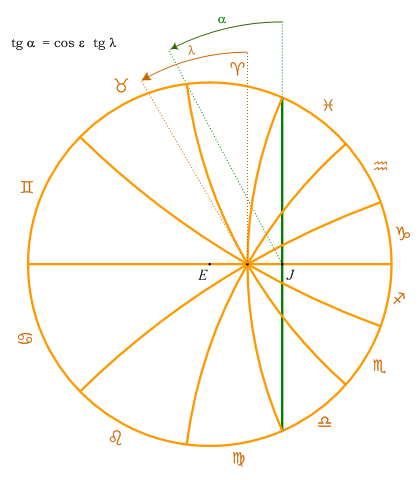
Scale of the Zodiac of the Orloj was not made in accordance with the stereographic projection. Individual signs are divided evenly in thirty degrees measured from the celestial South Pole (J). Such a division is justified on the clock where the angular velocities are constants. In that case ecliptic longitudes of the Sun and Moon rise evenly over time, being the so-called mean longitudes. The difference between the actual and mean longitude of the Sun is mainly due to eccentricity of the orbit of Earth, and can reach ± 1.9°. If the marks were derived from the stereographic projection, the difference between the real and displayed longitude of the Sun would amount to 4.1° (angular equivalent of the peak value of the Time Equation).
Digital model shows the true, not mean Sun. To ensure the longitudes subtracted on the model reflects the actual ecliptic longitudes, the scale derived from the stereographic projection is used. The following animation shows the difference between the two scales. The first one is uniform, used on the Orloj.

The question arises as to whether this was done in the past. A copy of the manuscript by Jan Taborsky "Report on the Astronomical Clock of Prague" was supplemented by texts in the 17th century, which include among others geometric drawings of the zodiac. Their scales correspond to the stereographic projection. It is likely that initially the clock was being set to the true solar time. In those days, the curator had to fix the clock often, possibly using the sundial to set the time.
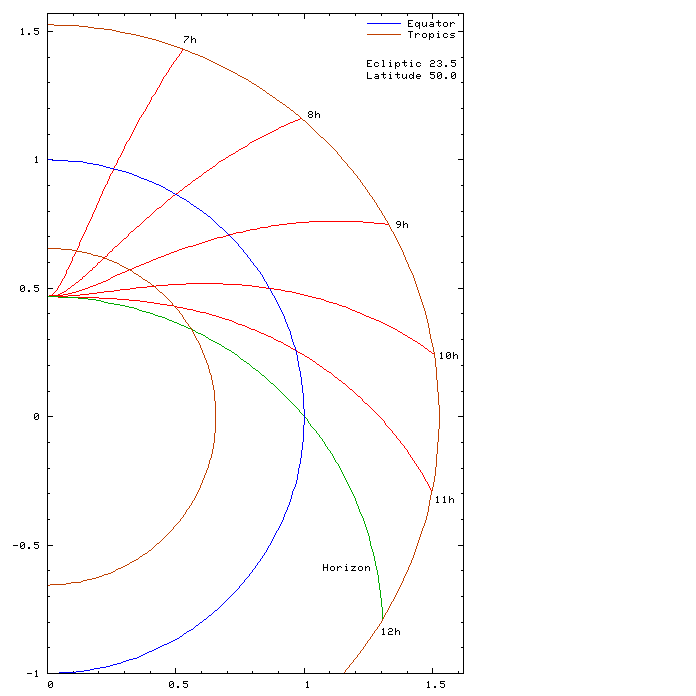
The time between sunrise and sunset is divided into twelve planetary hours so called from the belief that the hours were in turn dominated by one of the planets. Their length changes during the year. Design of the points of planetary curves is shown on the sun daily track divided into twelve equal segments during the equinoxes and solstices. The curves interpolated here make part of the circles, which differ only a little from the exact planet curves between the equator and the tropics. As you can see from the chart below, the difference is noticeable only near the southern point of the horizon. However, this area is not displayed on the astrolabe.
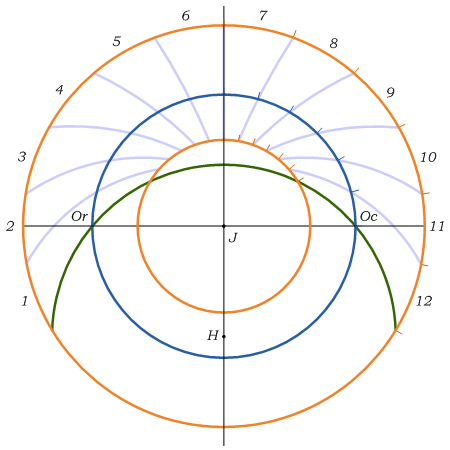
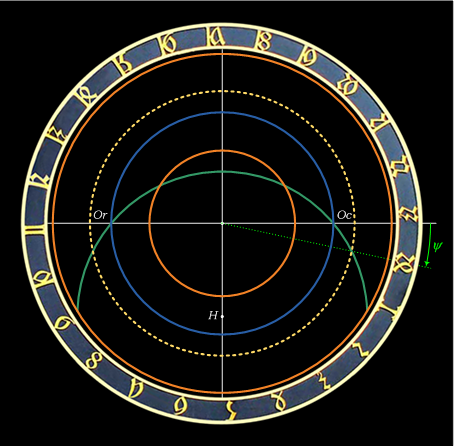
Old Bohemian day is divided into 24 equally long hours and begins at sunset. The dial of the Bohemian hours (called čtyřiadvacetník or twentyfour-er) turns a bit from day to day so that the sun hand points to 24 hours mark at sunset. Rotation angle of čtyřiadvacetník depends on the declination of the Sun, the daily arc of which has radius
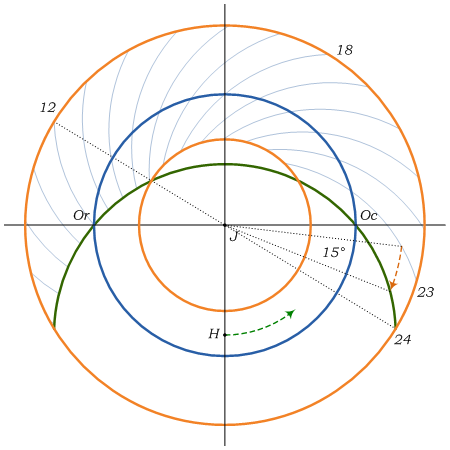
Reading of the Bohemian hours on the Prague Orloj is done using the čtyřiadvacetník. The same would be possible also using the system of circles positioned in the place of planetary curves. At the moment of sunset the Sun crosses the western part of the horizon; it is 24 Bohemian hours. The Sun is at the same declination circle an hour before sunset, only its hour angle is just by 15° smaller. Each day an hour before sunset the Sun can be found on the part of the circle formed by rotating the western part of horizon about 15° against the direction of daily movement. This system is described in the copy of the "Report on the Orloj ..." dating from the 17th century.
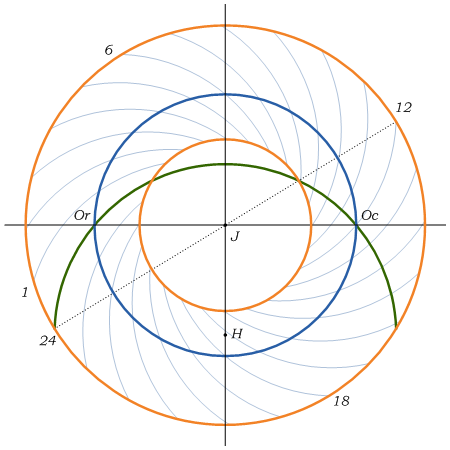
According to the terminology used to describe a sundial, Babylonian hours are equal hours obtained by dividing the day into 24 equal parts starting at sunrise. Design of curves that enable us to read Babylonian hours is analogous to the one which were used for Bohemian hours. The only difference is that now we use the eastern part of the horizon and rotations are clockwise.
The grid noticeable in the pictures of the astronomical clock in 1743 and 1793 years is not similar to symmetric planetary curves. It is possible, that after a certain period these curves were replaced by a grid of Babylonian clock. Thus, the Orloj made possible to read for both equal time from sunrise (through a grid of Babylonian clock), and from sunset (at twentyfour-er). On these pictures is also still visible a supplement to the original planetary curves – the table of individual rulers of the planetary hours (astrological domes) for each weekday placed above the windows, where are the apostles today. Departure from the astrological symbolism could be related to the expanding influence of Catholic education. In the nineteenth century the planetary curves were restored, but already the table lacks.
The approximations used to calculate the positions of the Sun and Moon are quite satisfactory given the size of the model. For example, the time interval used for the calculation of ecliptic longitudes should be different than the interval for the calculation of sidereal time. From the epoch J2000.0 only two leap seconds were inserted and not accounting for them has negligible consequences.
| d | = Number of days from the epoche J2000.0 = Jan 1 12:00 UT 2000 |
| S | = | 280.461 + 360.98564737*d + 14.421 | Local sidereal time [°] |
| Ls | = | 280.461 + 0.98564736*d | Mean longitude of the Sun [°] |
| Ms | = | 357.529 + 0.98560028*d | Mean anomaly of the Sun [°] |
| λs | = | Ls + 1.914sin(Ms) + 0.020sin(2Ms) + ... | Longitude of the Sun [°] |
| αs | = | λs – 2.465sin(2λs) + 0.053sin(4λs) + ... | Rectascension of the Sun [°] |
| δs | sin δs = sin ε sin λs | Declination of the Sun |
| Lm | = | 218.316 + 13.17639648*d | Mean longitude of the Moon [°] |
| Mm | = | 134.963 + 13.06499295*d | Mean anomaly of the Moon [°] |
| F | = | 93.272 + 13.22935024*d | Moon's argument of latitude [°] |
| D | = | Lm – Ls | Mean elongation of the Moon [°] |
| λm | = | Lm + 6.289sin(Mm) + 0.214sin(2Mm) + 1.274sin(2D – Mm) + 0.658sin(2D) – 0.185sin(Ms) – 0.114sin(2F) + ... | Geocentric longitude of the Moon [°] |
| αm | = | λm – 2.465sin(2λm) + 0.053sin(4λm) + ... | Rectascension of the fictitious Moon [°] |
Like the Orloj itself, this model doesn't take into account the inclination of the moon's orbit to the ecliptic (5,1°). As a consequence, the longitude and rectascension of the model can't be true simultaneously. The model displays geocentric longitude of the Moon. A new moon thus corresponds to the conjunction in longitude. On the other hand, geocentric rectascension of the Moon may differ from that which is displayed by as much as ± 2,1° and the moments of culmination may be in error up to 8 minutes.